03 Feb 2020 - Rahul Venugopal

Discrete random variable

X is a function from the outcomes to the real line

For example: RV is a function which is mapping sample space’s individual outcomes to numbers

We have probabilities associated with these random variables

Sum of all probabilities equals one. $\sum_{i=1}^{n}p_i=1$ and Sample space of $X$ is $S$

Self information, $i(p(x_j))=-log_2$ $p(x_j)$ bits

Weighted average of this self information gives us entropy, $H(X)$. Weights are the probabilities $p(x_i)$

$H(X)=E(-log$ $p(x))$

Definition of expectation of X: $E(X)=\sum_{i=1}^{n}p(x_i)$

$x_i = x1,x2,……x_n$ with probabilities $p1,p2,…..p_n$

$E(X)$ will give us average loss/gain if we take the example of gambling

History and Motivation

Axioms of entropy

Axiom 1

$H(p_1,p_2,p_3,…….p_n)\geqslant 0 $

The entropy of a random variable with n discrete outcomes of probabilities $p_1,p_2,….p_n$ will always be greater than or equal to zero

Axiom 2

$H(X)$ will be continuous in $p(S)$

Even if we perturb the probability values, the entropy cannot change drastically

Axiom 3

Let us take $n$ outcomes which are equally likely (coin toss or rolling a dice) and when $n$ increases, then the function $H(X)$ also increases monotonically with $n$

As per this axiom, the entropy of an unbiased coin is less than the entropy of an unbiased die

The uncertainty in choosing an outcome of die is more since there are larger number of states and hence more information/entropy

Axiom 4

There are two random variables $X$ and $Y$ and if they are independent, the joint entropy, $H(X,Y)$ is the sum of their individual entropies $H(X)$ and $H(Y)$. The entropy gets added up.

Say, $X$ is a random variable (tossing a coin) and $Y$ is the random variable (rolling a dice), the uncertainty in rolling the dice remain intact even if know uncertainty in tossing the coin. Knowing head or tails of the coin won’t help in reducing the uncertainty in the numbers which comes out from rolling dice

Mutual information, $I(X,Y)$ comes into picture when $X$ and $Y$ are not independent

Axiom 5 - Grouping axiom

We begin with a set of random variable, $x_i$ with probabilities $p_1,p_2,p_3,…..p_n$

The set is now broken into two sets. Set A and Set B. A and B are disjoint sets with probabilities

$p(A)={p_1,p_2,p_3,…….p_r}$ and $p(B)=p_{r+1},p_{r+2},+…….p_n$.

$p(A)+p(B)=1$

The grouping axiom says that, the entropy of the entire set can be written as:

\[H(p(A),p(B))+p(A)*H(\frac{p_1}{p(A)},\frac{p_2}{p(A)},.....\frac{p_r}{p(A)}) +p(B)*H(\frac{p_{r+1}}{p(B)},\frac{p_{r+2}}{p(B)},.....\frac{p_n}{p(B)}\]

To find the uncertainty of an outcome, first we are going to list the outcome either in A or in B

Once we list the outcome in say set A, we need to think only about of uncertainty within A (out of r outcomes). This approach is like divide and conquer

The new probabilities are more like conditional probabilities. The breaking can also be into sets of three or four. We have to compute, the conditional probabilities accordingly

We are trying to index every outcome. First level of indexing is whether outcome belongs to set A or B. Second level of indexing would be within A or within B. Multiple level or nested indexing are also possible and axiom would still hold

Summary

What Shannon showed was

\[H(p_1,p2,p_3,...p_n)=-k\sum_{i-1}^{n}p_i*\log p_i \text{ bits}\]

Only this equation satisfies all the five conditions in above axioms of entropy

$k$ varies when the base of logarithm changes

Conditional entropy

Let us say we have $x_i$ and $y_j$ as two outcomes

$I(x_i/y_j)$ is called conditional self information of $x_i/y_j$ which is expressed as $-log_2 $ $p(xi/yj)$

We have two random variables $x$ and $y$ where $x_i = x_1,x_2,…x_n$ and $y_j = y_1,y_2,…y_m$

Conditional entropy, $H(X|Y)$ = $\sum_{i=1}^{n}\sum_{j=1}^{m}p(x_i,y_j)*-log p(x_i/y_j)$ bits

$p(x_i,y_j)$ is the joint probability density function or joint probability mass function

The weights are joint probabilities, we have to know the probability of how they occur together

We need the joint PDF to calculate the expected value

When $x_i $and $y_j$ are independent random variables it means that all pairs of $x_i$ and $y_j$ are independent

$H(X Y) = \sum_{i=1}^{n}\sum_{j=1}^{m} p(x_i)p(y_j)*-log(p(x_i))$

​ $=\sum_{j=1}^{m} p(y_j)\sum_{i=1}^{n}p(x_i)*-log(p(x_i))$

$=1*H(X)$ bits

Knowing $Y$ doesn’t help to improve uncertainty in $X$, $H(X)$

$H(X|Y)$ means what is the uncertainty in X after knowing $Y$. The uncertainty in $X$ remains the same even before knowing $Y$ and after knowing $Y$ when $X$ and $Y$ are independent

If $x_i$ and $y_j$ are completely dependent, $p(x_i/y_j)=1$. Then,

$H(x_i|y_j)$ = 0 bits

When $x=f(y)$ and $f$ is deterministic OR a table lookup. Given that $y$ has occurred, we can find everything about $x$. There is no uncertainty in $x$ once $y$ is known

This can happen when $X$ and $Y$ are mutually exclusive also

But, if $x$ is a stochastic function $f(y)+\epsilon$, then there will be some uncertainty around $x$ even after knowing $y$

$H(Y|X)$ not equal to $H(Y|X)$ These are not symmetric/commutative
$H(X)>= H(X|Y)$ This is an important relation

Knowing $Y$, $H(X|Y)$ can always be equal or less than $H(X)$

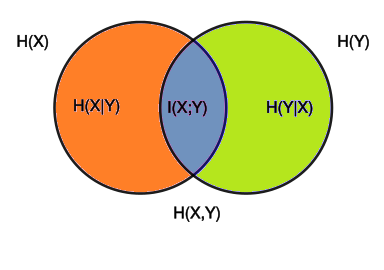
Mutual Information - I(X,Y)

$I(X,Y)$ is defined as mutual information

$I(X,Y) = I(Y,X)$ Mutual information is symmetric. Sometimes one of this will be easy to compute.

Mutual information tells us what information is common between X and Y random variables

Consider $x$ as input to a channel and $y$ as output (The channel can be a neuron/synapse or a cable), then the mutual information is the information which is transmitted through the channel

IF $x_i$ and $y_j$ are independent then $p(xi/yj)=p(xi)*p(yj)$. Nothing is common between these two outcomes

$I(x,y)= 0$ bits when they are independent

If $x_i = f(y_j)$, then $I(x_i,y_j) = log(1/p(x_i))$ = $-log$ $p(x_i)$

This is self information of $x_i$

IF the channel is deterministic, whatever uncertainty in X is transmitted via the channel just like that

Mutual information can be visualised as the quantity of information that is transferred reliably across the channel. The uncertainty comes through just like that, that is the best we can do in terms of improving the channel

If the channel is carrying zero information, it is a terrible channel

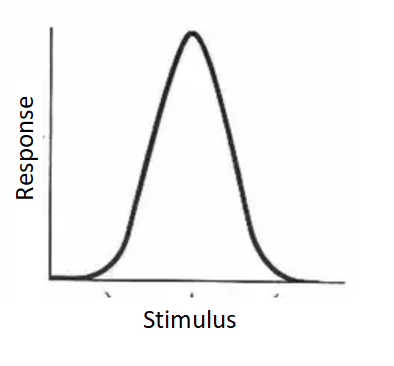
This book provides a self-contained review of relevant concepts in information theory and statistical decision theory. This book discuss the topic of stimulus response curves. There is a particular stimulus which gives maximum response value. How much information of the stimulus is conveyed by the response is represented as a stimulus-response curve.

Proof for symmetry property of mutual information

$I(X,Y)=\sum_{i=1}^{n}\sum_{j=1}^{m} p(x_i,y_j)*log(\frac{p(x_i/y_j)}{p(x_i)})$ bits

​ \(=\sum_{i=1}^{n} \sum_{j=1}^{m} p(x_i,y_j)* \log(p(x_i/y_j) - \sum_{i=1}^{n}\sum_{j=1}^{m}p(x_i,y_j)* \log(p(x_i))\)

​ \(=\sum_{i=1}^{n}\sum_{j=1}^{m}p(x_i,y_j)* \log(p(x_i/y_j) - \sum_{i=1}^{n}\log(p(x_i)) \sum_{j=1}^{m}p(x_i,y_j)\)

​ \(= -H(X\|Y)+H(X)\)

​ $I(X,Y)=H(X)-H(X|Y)$

Mutual Information,$I(X,Y)$ = Entropy in X, $H(X)$ minus uncertainty in $H(X)$ after knowing $Y$

$\sum_{j=1}^{m}p(x_i,y_j)=\sum_{j=1}^{m}p(y_j/x_i)*p(x_i)$

​ $=p(x_i)\sum_{j=1}^{m}p(y_j/x_i)$

​ $=p(x_i)*1$

Similarly, $I(Y,X)=H(Y)-H(Y|X)$

This can be proved by multiplying and dividing by $p(y_j)$

\[I(X,Y)=\sum_{i=1}^{n}\sum_{j=1}^{m}p(y_j,x_i)*\log\big[\frac{p(y_j/x_i)}{p(y_j)}*\frac{p(y_j)}{p(y_j)}\big]\]

​ $=I(Y,X)$

​ $=I(Y,X)=H(Y)-H(Y|X)$

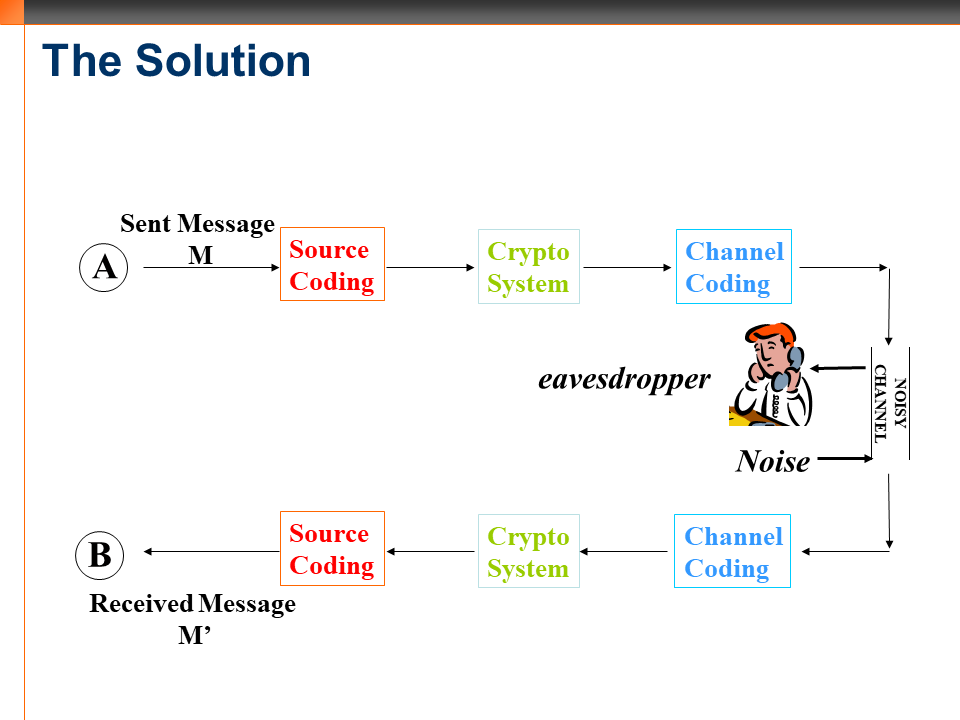
How to transmit information efficiently, securely across a noisy channel

Efficiency, security and reliability of the channel are three key things when we transmit information from point A to point B. These two points can be space,time or space-time

The receiver has to revert/inverse these steps to recover back information

Compress –> Lock –> Error correcting coding –> Error correction decoding –> Unlock –> Decompress These are the steps followed from point A to point B. The three major steps need not be there always in an information transfer. Example: Storing passwords in computer. We might not need encryption or compression. We can have all combinations of these three fundamental chains of communication- Compression, Encryption and Error correction

Summary

Entropy

Boltzmann’s tombstone has the second law of thermodynamics carved in

Shannon’s 1948 paper covered source coding and error correction. 1949’s paper covered encryption

Entropy is that

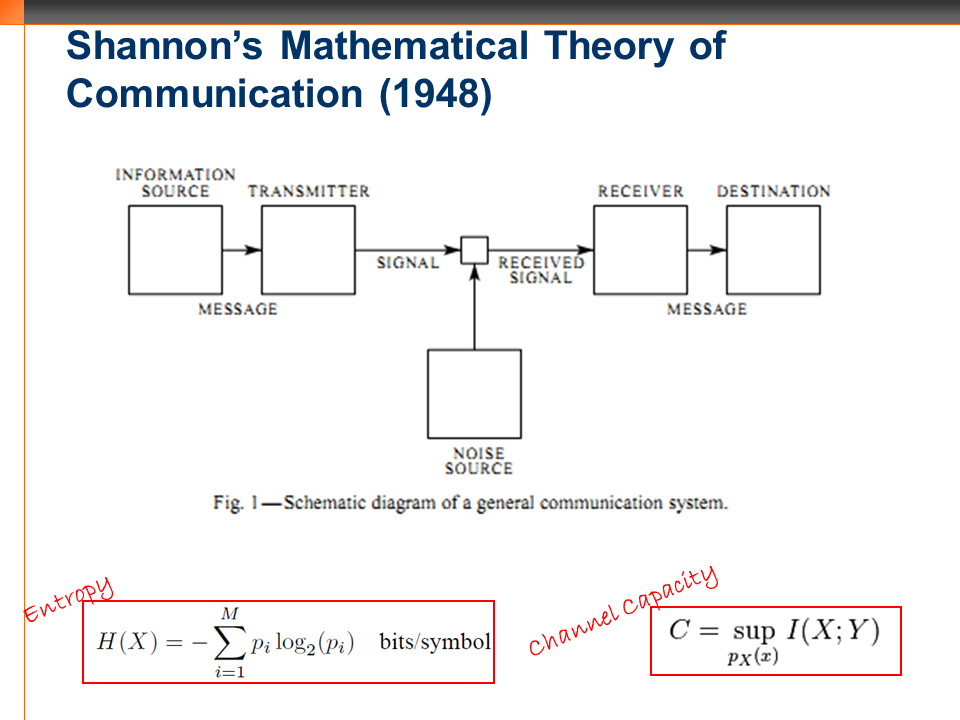
Entropy is that part of energy which cannot be converted to work. Shannon is the father of cybernetics. He designed a mechanical mouse which could adaptive learn maze travel. He even came up with a juggling theorem

The word bit was attributed to John Tuckey of Bell labs. Even Nyquist theorem is actually Shannon-Nyquist theorem