18 Feb 2020 - Harikrishnan N B
Effiiciency
Efficiency of a code ($C$) is defined as
\(\begin{equation} \eta = \frac{H(X)}{L(C)} \end{equation}\) where $H(X)$ is the entropy of the message symbols and $L(C)$ is the average code word length. Also, $0 \leq H(X) \leq L(C)$, this implies $0 \leq \eta \leq 1$.
- Find $H(X)$, $L(C)$ and $\eta$ for the example in Table I (Use Huffman code to find the code word of alphabet):
Table I: Compute the efficiency.
| Alphabet | Probability |
|---|---|
| A | 0.9 |
| B | 0.1 |
Now, how to improve the efficiency of code by still using the huffman code.
This can be done by creating a different alphabet. The different alphabet is obtained by taking two at a time (i.e AA, AB, BA, BB). Here we assume independence, so the probability of A and A is $P(A)\times P(A) = 0.81$. Similarly for AB, BA and BB. Table II shows the new alphabet and its corresponding probabilities.
Table II: Compute the efficiency.
| Alphabet | Probability |
|---|---|
| AA | 0.81 |
| AB | 0.09 |
| BA | 0.09 |
| BB | 0.01 |
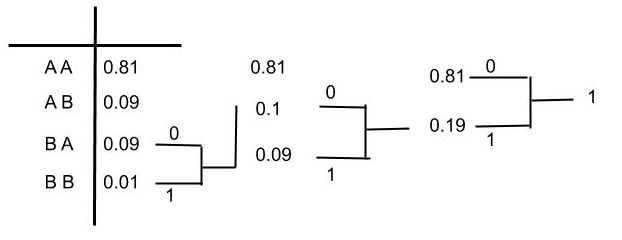
Figure 1: Computing Huffman code for the example in Table II.
Table III : Huffman Code for the example in Table II.
| Alphabet | Probability | Codeword |
|---|---|---|
| AA | 0.81 | 0 |
| AB | 0.09 | 11 |
| BA | 0.09 | 100 |
| BB | 0.01 | 101 |
In this case, the average code word length $L_{new}(C) = 1 \times 0.81 + 2 \times 0.09 + 3 \times 0.09 + 3 \times 0.01 = 1.29$ bits/pair.
$L_{new}(C)$ per symbol $= \frac{1.29}{2} = 0.645$ bits/symbol.
Since we assumed independence of A and A, A and B, B and A, B and B, therefore $H_{new}(X) = 2 \times H(X)$ bits/pair.
$H_{new}(X)$ per symbol $= H(X) = 0.46$ bits/symbol
Therefore, $\eta_{new} = \frac{H_{new}}{L_{new}(C)} = \frac{ H(X)}{L_{new}(C)} = \frac{ 0.46}{ 0.645} = 0.71$ bits/symbol.
The above concept is called blocking. Here we used a block size = 2. Blocking increases the efficiency. The disadvantage of blocking is the storage of more symbols. For example if there are 26 input alphabet and if we use a blocksize $=2$, then we need to store $26^{2}$ new alphabets. Blocking always increases the efficiency but the storage of new alphabets is the constraint. Blocking is true for Shannon-Fano coding as well.
Source Coding Theorem
What is the best possible $L(C)$?
For a discrete memoryless source it is possible to construct a prefix free code $C$, whose average codeword length $L(C)$ is $H(X) \leq L(C) < H(X) + 1$.
Proof
$H(X) \leq L(C)$
Consider $H(X) - L(C) = - \sum_{i =1}^{L} p_{i} \log_{2}(p_i) - \sum_{i =1}^{L} p_{i} n_{i}$ where $n_1, n_2, \ldots, n_L$ are codeword length of a prefix free code $C$.
\[\begin{align*}H(X) - L(C) &= \sum_{i = 1}^{L} p_{i} \log_{2}(\frac{1}{p_i}) + \sum_{i =1}^{L} p_i \log_{2}2^{-n_i} \\ H(X) - L(C) &= \sum_{i = 1}^{L} p_i \log_2 \bigg(\frac{2^{-n_i}}{p_i}\bigg)\end{align*}\]Using the inequality,
\[\sum_{i = 1}^{L} p_i \log_2 (\frac{2^{-n_i}}{p_i}) = \frac{1}{\ln(2)}\sum_{i=1}^{L}\ln(\frac{2^{-n_i}}{p_i} )\leq \frac{1}{\ln(2)} \sum_{i=1}^{L} p_i (\frac{2^{-n_i}}{p_i} - 1)\]On further simplification we have,
\[\sum_{i = 1}^{L} p_i \log_2 (\frac{2^{-n_i}}{p_i}) = \frac{1}{\ln(2)}\sum_{i=1}^{L}\ln(\frac{2^{-n_i}}{p_i}) \leq \frac{1}{\ln(2)}(\sum_{i=1}^{L} 2^{-n_i} - \sum_{i=1}^{L} p_i )\] \[\sum_{i = 1}^{L} p_i \log_2 (\frac{2^{-n_i}}{p_i}) = \frac{1}{\ln(2)}\sum_{i=1}^{L}\ln(\frac{2^{-n_i}}{p_i}) \leq \frac{1}{\ln(2)} \sum_{i=1}^{L} 2^{-n_i} - 1\]By Krafts Inequality,
\[\sum_{i=1}^{L} 2^{-n_i} \leq 1\]As a result,
\[H(X) - L(C) \leq 0\]Second part of Proof
\[L(C) < H(X) + 1\]Choose a codeword such that $2^{-n_i} \leq p_i < 2^{-n_i + 1}$, $\forall i = 1, \ldots, L$ and $p_i \neq 0$.
$n_1, \ldots n_L$ are the codeword lengths.
Choosing $n_i$ such that for every $p_i$ the following is true:
\[\begin{align*}\underbrace{\sum_{i=1}^{L}2^{-n_i} \leq \sum_{i=1}^{L}p_i} &< \sum_{i=1}^{L}2^{-n_i + 1} \\ \sum_{i=1}^{L}2^{-n_i} \leq 1 \end{align*}\]satisfies the Kraft’s Inequality. This implies there are codewords which are prefix free.
From the assumption we have,
\[2^{-n_i} \leq \underbrace{p_i < 2^{-n_i + 1}}\]Take $\log$ on second part of inequality.
\[\begin{align*}\log_{2} p_i &< \log_{2} 2^{-n_i + 1} \\ \log_{2} p_i &< -n_i + 1 \\ n_i &< -\log_{2}p_i + 1\end{align*}\]Multiply by $p_i$ on LHS and RHS,
\[\begin{align*} p_{i}n_{i} &< -p_{i}\log_{2}p_{i} + p_{i} \\ \sum_{i = 1}^{L}p_{i}n_{i} &< - \sum_{i=1}^{L}p_{i}\log_{2}p_i + \sum_{i = 1}^{L}p_i\\ \implies L(C) &< H(X)+1 \end{align*}\]The above suggests that good code word exists.