02 Mar 2020 - Abhishek Nandekar

A Motivation to Channel Coding:

Channel Coding and Error Control Coding is considered as the third pillar of Information Theory, akin to Source Coding or Data Compression and Encryption or Cryptography. It owes its importance to the noise that an interfere in the transmission channel of Information flow.

Error: An error occurs when the transmitted bit is not the same as the received bit. The aim of Channel Coding is to detect and correct these errors.

Hence, Channel Coding is essentially a pre-processing of the data before transmission. Redundancy is added to Information. The output is longer than the input.

Repetition Codes:

Let’s say we want to transmit the message 010110. Then, in a $\mathbb R_3$ repetition code, every bit is repeated thrice, making the new message to be transmitted 000 111 000 111 111 000. Now let’s say we receive 000 101 100 111 001 000. So, on the decoder side, we count the majority bit in every group of 3 bits. So, after decoding, the received message becomes 010100, which is very close to the actual message 010110, even after 4 errors occurred in transmission. Typically, consecutive errors do not occur in most of the channels.

Error Detection and Correction:

Why Error Detection?

Error detection is less computationally intensive, and once you know that the error has occurred, transmission can be repeated and the average of the two received Codes can reduce the error.

Parity bit:

Consider a block of 0’s and 1’s, and append this block with a 0 if there are odd number of 1’s in the message.

Channel Coding techniques can only detect accidental errors, such as corruption of stored data or transmission. They cannot handle attacks by a malicious agent.

Examples:

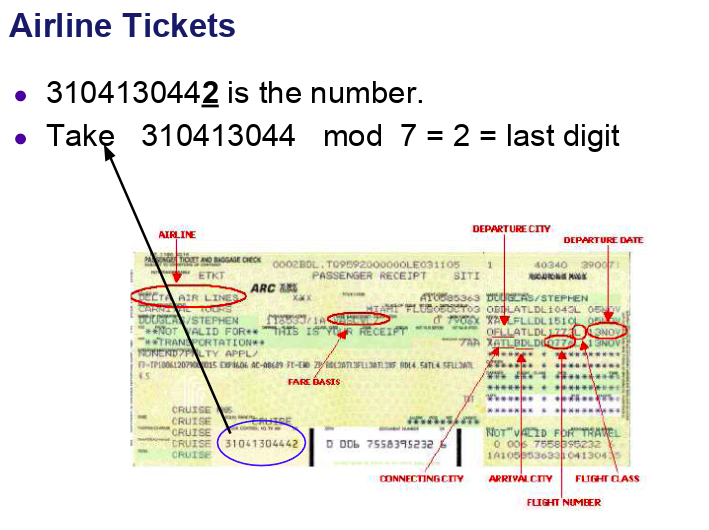
Airline Ticket

In the above figure, 310413044 is appended with 310413044 mod 7 = 2. So, if the ticket is counterfeit, there will be an algorithm that checks this. So, if there is a typing mistake or some other accidental error in the ticket number, it’ll get detected instantly.

Another example are International Standard Book Numbers(ISBN)

ISBN
As we can see, divisibility by 11 is checked here.

Hence, the intuition behind Channel Coding is modelling the channel and predict the likeliness of occurrence such accidental errors.

Mathematical Model of a Channel:

Information can be transmitted via a plethora of channels like neural synapses, air, cosmic space, coaxial cable, a compact disc etc.

To model a channel, consider a function that takes as input an alphabet sequence $\{a_1, a_2 \ldots, a_r\}$ with probabilities $\{p_1, p_2, \ldots, p_r\}$, and returns as output another alphabet sequence $\{b_1, b_2, \ldots, b_s\}$, with probabilities $\{q_1, q_2, \ldots, q_s\}$. For the sake of simplicity, a binary model is assumed. But the theory will hold for other types of alphabets too.

Assumptions:

The transition probabilities of a channel are defined as:
\(Q_{j|i} = P(Y=b_j|X=a_i)\)

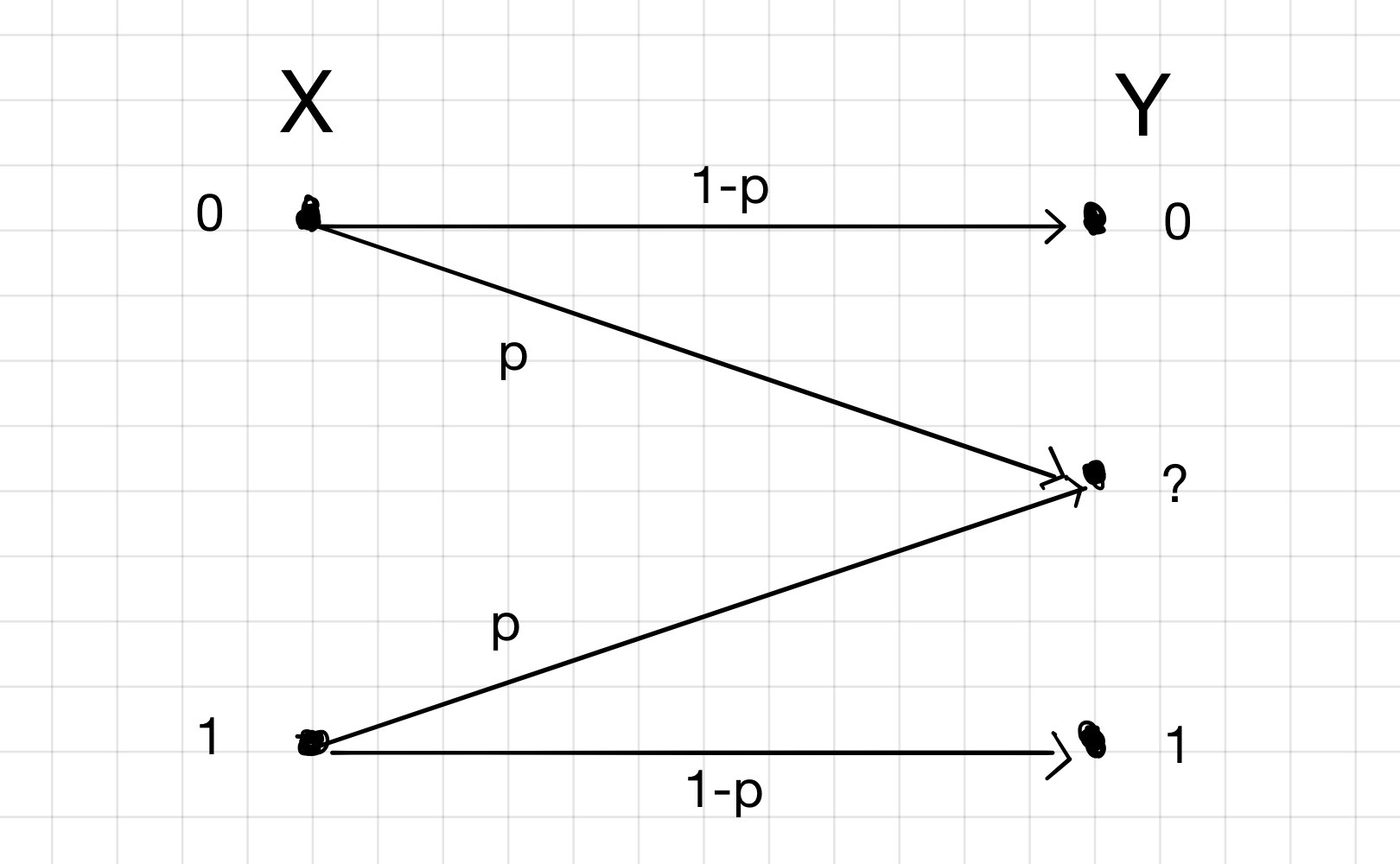
Binary Symmetric Channel(BSC):

This model is one of the most important examples of Channel Coding. BSC Let the input alphabets be 0 and 1 and possible output alphabets also be 0 and 1. Then, here, $p$ is the probability that 1 is received as the output when 0 was transmitted, and vice-versa.

Hence, the probability of error $p$: \(\implies p = P(Y= 0 | X = 1) = P(Y=1|X=0)\)

This channel is called a symmetric channel because of the fact the $P(Y=0|X=1) = P(Y=1|X=0)$. In general, this is not always true. Hence, the transition matrix can be formulated as: \(Q = \begin{bmatrix} 1-p & p \\ p & 1-p \end{bmatrix}\)

Hence, \(Q_{ij} = P(Y=i|X=j)\) where $i, j \in \{0, 1\}$.

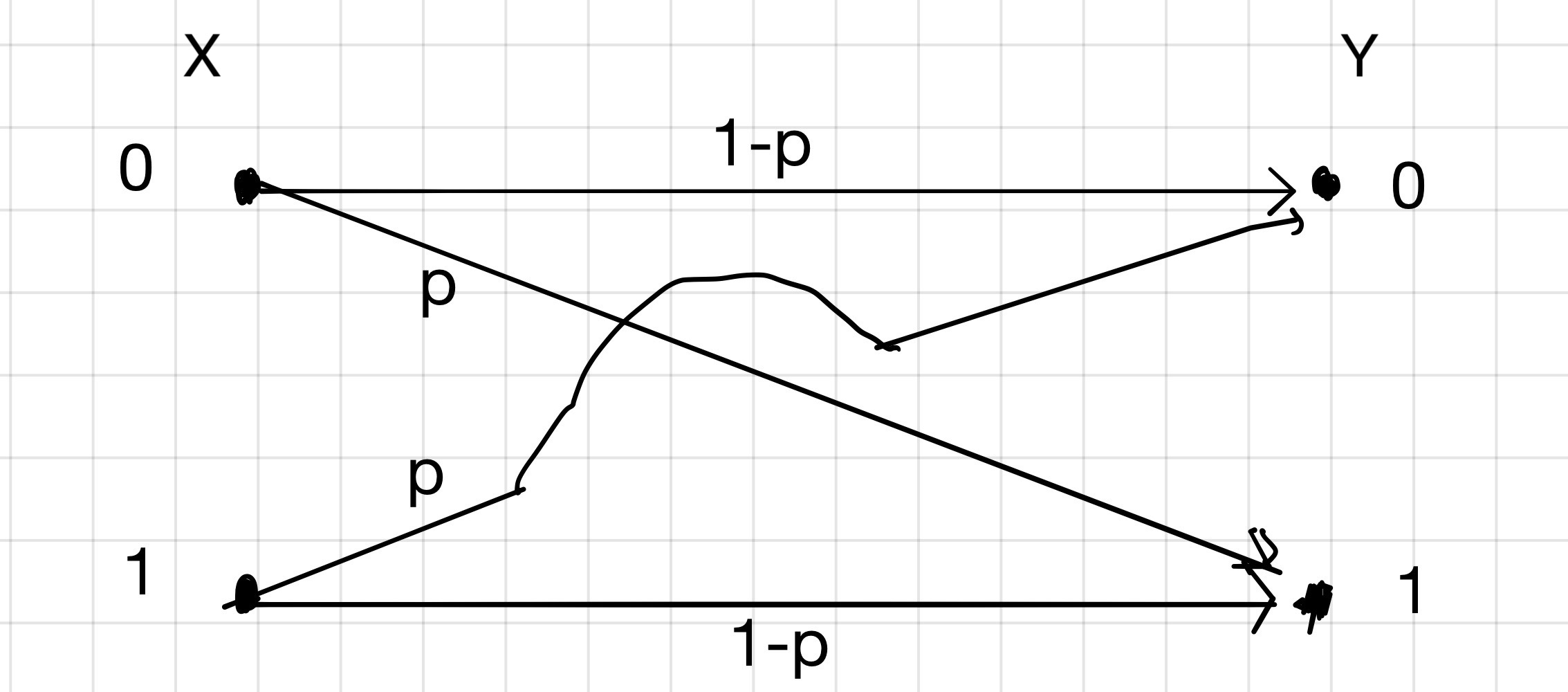
Binary Erasure Channel(BEC):

There are channels that violate the first assumption we made above. One such channel is the Binary Erasure Channel(BEC). BEC

As we can see, in this channel, 0 will be sent as 0 or will be erased, 1 can be sent as 1 or erased. Here, the transition matrix can be defined as: \(Q = \begin{bmatrix} 1-p & 0 \\ p & p \\ 0 & 1-p \end{bmatrix}\)

Hence, \(Q_{ij} = P(Y=i|X=j)\)
where $i \in \{0, ?, 1\}$ and $j \in \{0, 1\}$.

In this article, all the calculations and derivations are performed assuming the BSC model, unless specified.

As explained in the examples above the transition probability matrix $Q$ is constant. Inferentially, we have a direct control over $X$, but $Y$ depends on the channel. So, all the calculations in Channel Coding will make that assumption.

Typically, in the absence of encryption, the output of Source Coding is the input to Channel Coding.

Why Channel Coding:

As we have seen above, the efficiency of the Channel is hard to control. So the central objective of Channel Coding is to pre-process the data in such a manner that maximum information is exchanged through the channel. Mathematically, we want to maximise $\mathbb I(X, Y)$.
\(\begin{align*} \mathbb I(X, Y) &= H(X) + H(Y) - H(X, Y) &\\ H(X) &= \sum_{i=1}^r p_i \log_2 \frac{1}{p_i} & p_i = P(X=a_i) \\ H(Y) &= \sum_{j=1}^s p_j \log_2 \frac{1}{p_j} & p_j = P(Y=b_j) \\ H(X, Y) &= \sum_{i=1}^r\sum_{j=1}^s R_{ij} \log_2 \frac{1}{R_{ij}} & R_{ij} = P(X=a_i, Y=b_j) \end{align*}\)
where, $H(X)$ is the amount of information being sent at input, $H(Y)$ is the amount of information received at the output, $H(X, Y)$ is the Joint information and $\mathbb I(X, Y)$ is known as the Mutual Information between input and output, which represents the amount of information communicated from the sender to the receiver. Some other applications of Mutual Information:

Example: Binary Symmetric Channel (BSC)

Suppose in a BSC channel, the probability of error $p = 0.1$, and $p_0 = P(X=0) = 0.2$ and $p_1 = P(X=1) = 1-p_0 = 0.8$.

Assume, 0 was received. Then: \(\begin{align*} p_{00} = P(X=0|Y=0) &= \frac{P(X=0, Y=0)}{P(Y=0)} \end{align*}\)
Applying Bayes Theorem,
\(\begin{align*} p_{00} = P(X=0|Y=0) &= \frac{P(X=0) P(Y=0|X=0)}{P(X=0)P(Y=0|X-0) + P(X=1)P(Y=0|X=1)} \\ &= \frac{0.2 \times 0.9}{0.2\times0.9 + 0.8\times 0.1} \\ &= 0.69 \end{align*}\)

The probabilities $P(X=0)$ and $p$ are independent. And $P(Y=0)$ and $P(Y=1)$ are two mutually exclusive events. Hence, their probabilities are added in the denominator.

Similarly, \(p_{10} = P(X=1|Y=0) = \frac{0.8\times 0.1}{0.2\times 0.9 + 0.8\times 0.1} = 0.31\)

Now, if 1 was received, then: \(\begin{align*} p_{01} = P(X=0|Y=1) &= \frac{P(X=0)P(Y=1|X=0)}{P(X=0)P(Y=1|X=0)+P(X=1)P(Y=1|X=1)}\\ &= \frac{0.2\times 0.1}{0.2\times 0.1 + 0.8\times 0.9}\\ &= 0.027 \end{align*}\)
And \(p_{11} = P(X=1|Y=1) = \frac{0.8\times 0.9}{0.2 \times 0.1 + 0.8\times 0.9} = 0.973\)

Hence,
\(\begin{align*} q_0 = P(Y=0) &= P(X=0)(1-p) + P(X=1)(p)\\ &= p_0(1-p) + p_1(p)\\ &= 0.2\times 0.9 + 0.8\times0.1\\ &= 0.26 \\ \text{And}\\ q_1 = P(Y=1) &= P(X=1)(1-p) + P(X=0)(p) \\ &= p_1(1-p) + p_0(p)\\ &= 0.8(0.9) + 0.2(0.1)\\ &= 0.74\end{align*}\)
where, $p$ is the probability of error.

Channel Capacity

The Channel Capacity of a channel can be defined as $C = \max_{p_0} \mathbb I(X, Y)$. Hence, for the above defined channel,
\(\begin{align*}C &= \max_{p_0}\mathbb I(X, Y) \\ &=\max_{p_0} H(Y) - H(Y|X)\\ \text{Define $H_2(f)$ as}\\ H_2(f)&= f\log_2\frac{1}{f} + (1-f)\log_2\frac{1}{1-f} & f \in (0, 1)\\ \text{Then }\\ H(Y)&= H_2(p_0p + p_1(1-p))\\ H(Y|X) &= p_0H(Y|X=0) + p_1H(Y|X=1)\\ &= p_0H_2(p) + p_1H_2(p)\\ &= H_2(p)\end{align*}\) \(\begin{equation} \label{eq:ChannelCap} \tag{1} \implies C =\max_{p_0}H_2(p_0p + p_1(1-p)) - H_2(p)\end{equation}\) The second term in the above equation is constant. Hence we need to maximise the first term. The Binary Entropy Function $H_2(f)$ is maximum when $f=0.5$.
\(\begin{align*}H_2(0.5) &= 0.5\log_2\frac{1}{0.5} + 0.5\log_2\frac{1}{0.5}\\ &= 1 \text{ bit}\end{align*}\)
Now, in equation \eqref{eq:ChannelCap} when $p_0 = 0.5$,
\(\begin{align*}H_2(p_0p + p_1(1-p)) &= H_2(0.5p + 0.5(1-p))\\ &= H_2(0.5)\\ &= 1\text{ bit}\end{align*}\)

Therefore,

\[\begin{align*}C &= \max_{p_0}H_2(p_0p + p_1(1-p)) - H_2(p)\\ &= 1 - H_2(p) \text{ bits}\end{align*}\]

In BSC presented in the previous section,

\[\begin{align*}H(X) &= p_0\log_2\frac{1}{p_0} + (1-p_0)\log_2\frac{1}{1-p_0}\\ &= 0.2\log_2\frac{1}{0.2} + 0.8\log_2\frac{1}{0.8}\\ &= 0.722 \text{ bits}\end{align*}\]

And,

\[\begin{align*}H(X|Y) &= \sum_{y\in Y}q_y H(X|Y=y)\\ &=\sum_{y \in Y} q_y(\sum_{x\in X}P(X=x|Y=y)\log_2\frac{1}{P(X=x|Y=y)}) \\&=q_0H(X|Y=0) + q_1H(X|Y=1)\\ &=q_0(p_{00}\log_2\frac{1}{p_{00}} + p_{10}\log_2\frac{1}{p_{10}}) + q_1(p_{10}\log_2\frac{1}{p_{10}} + p_{11}\log_2\frac{1}{p_{11}})\\ &= 0.26(0.69\log_2\frac{1}{0.69} + 0.31\log_2\frac{1}{0.31}) + 0.74(0.027\log_2\frac{1}{0.027} + 0.973 \log_2\frac{1}{0.973})\\ &= 0.26(0.89) + 0.74(0.18)\\ &= 0.365\text{ bits}\end{align*}\]

Hence, Channel Capacity $C$ is:
\(\begin{align*}C &= H(X) - H(X|Y)\\ &= 0.722 - 0.365 \text{ bits}\\ &= 0.357 \text{ bits}\end{align*}\)