23 Jan 2020 - Pranay Yadav
Fourth Proof for the infinitude of primes using calculus
Proof by contradiction
Strategy: Assume that the number of primes is bounded and use the natural logarithm to undermine this bound.
Bound: The number of primes less than or equal to a real number $z$, given by
\[\pi(z) :=\#\{p\le z:p\in\mathbb{P} \}, \text{ where }\mathbb{P}\text{ is the set of primes }p_1,p_2,p_3\ldots\]Steps:
- The natural logarithm is monotonically decreasing
- Left Riemann sum approximation of the natural logarithm corresponds to the harmonic numbers
- Fundamental theorem of arithmetic
- Tricks of bounds
1. The natural logarithm is monotonically decreasing
The natural logarithm is defined as:
\[\ln{x}=\int_{1}^{x}\frac{1}{t}dt = \int_{1}^{x}f(t)dt, \text{ where } f(t)=\frac{1}{t}dt\]The first and second derivatives of $f(t)$ are:
\[f'(t) = -\frac{1}{t^2}\qquad\text{and}\qquad f''(t) = \frac{2}{t^3} \\ \forall{t>1},\ \ f'(t) < 0\ \text{ and }\ f''(t) > 0\]Thus, $f(t)$ has a negative slope and is convex everywhere for $t>1$ and is monotonically decreasing.
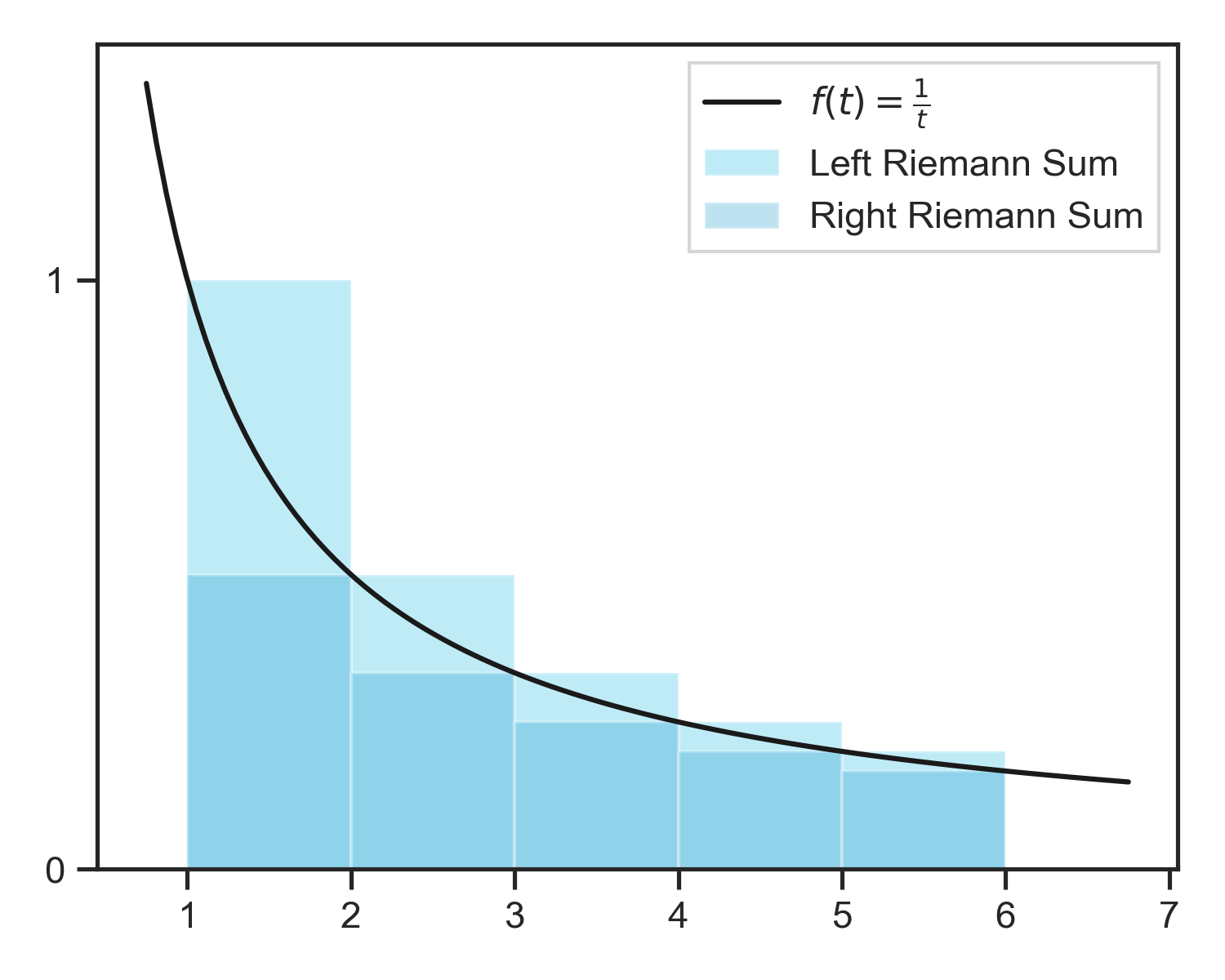
2. Left Riemann sum approximation of the natural logarithm
Consider the points $a,\ b,\ x$ as values of $t$ for the function $f(t)$ such that $a \le x \le b$:
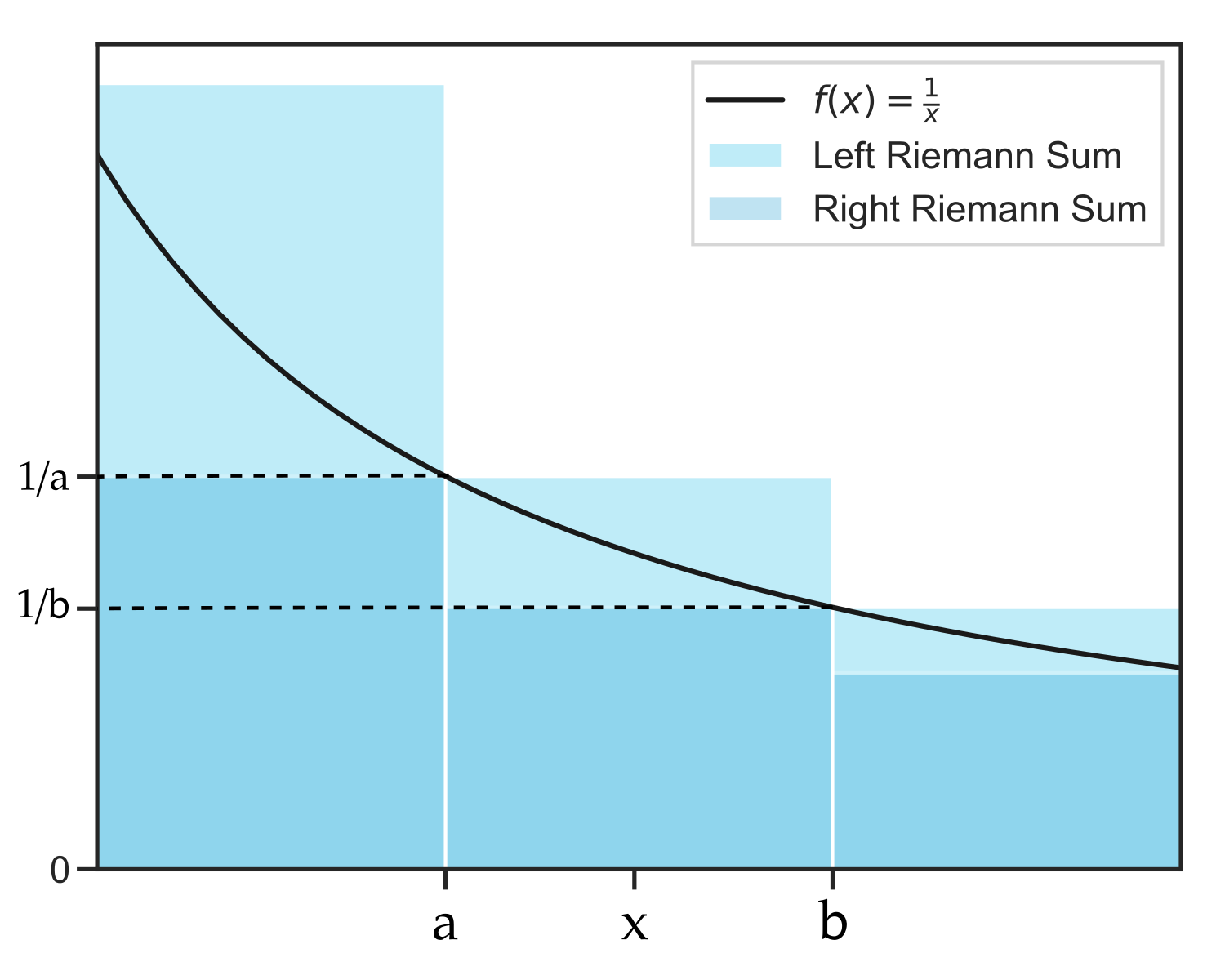
Since $f(t)$ is monotonically decreasing,
\[f(a)\ge f(x) \ge f(b) \\ \int_a^b f(a) \ge \int_a^b f(x) \ge \int_a^b f(b) \\ \text{the integral corresponds to the area enclosed in the rectangles} \\ \frac{b-a}{a} \ge \int_a^b f(x) \ge \frac{b-a}{b} \\ \text{Left Riemann Sum} \ge \int_a^b f(x) \ge \text{Right Riemann Sum}\]The above can be generalized to the integral and its approximation for $f(t)$ from $1$ to $x$ as:
\[\text{Left Riemann Sum} \ge \int_1^x f(t) \ge \text{Right Riemann Sum}\]Focusing on the Left Riemann Sum and by the definition of the logarithm:
\[\ln{x}\le \text{Left Riemann Sum approximation}\]Consider the upper bound on prime numbers $z$, such that $n\le z < n+1$ for some $n$:
\[\ln{z} \le 1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{n-1} +\frac{1}{n}\\\text{(width of each rectangle in Riemann sum = 1)}\]Since all the numbers $1,2,\ldots,n$ are $\le z$ (since $n\le z$ ), they have only prime divisors $\le z$. If we consider all possible numbers that can be formed using only primes less than $z$, then the sum of these will be larger than the sum above.
\[1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{n-1} +\frac{1}{n} \le \sum\frac{1}{m}\]where $m\in\mathbb{N}$ such that they only have prime divisors $p\le z$. Thus
\[\ln{z} \le \sum\frac{1}{m}\]3. Fundamental theorem of arithmetic
By the fundamental theorem of arithmetic, each $m$ can be written in a unique way as a product of primes:
\[m=\prod_{p\le z}p^{k_p}\]Therefore,
\[\ln{z} \le \sum\frac{1}{m} = \sum\frac{1}{\prod_{p\le z}p^{k_p}}\]Taking the above equation with only 2 primes $p_1, p_2$ and expanding, we get
\[\sum\frac{1}{m}=1+\frac{1}{p_1}+\frac{1}{p^2_1}+\frac{1}{p^3_1}+\ldots \\ \qquad \qquad \frac{1}{p_1p_2}+\frac{1}{p^2_1p_2}+\frac{1}{p^3_1p_2}+\ldots \\ \qquad \qquad \frac{1}{p_1p^2_2}+\frac{1}{p^2_1p^2_2}+\frac{1}{p^3_1p^2_2}+\ldots \\ \sum\frac{1}{m}=(1+\frac{1}{p_1}+\frac{1}{p^2_1}+\frac{1}{p^3_1}+\ldots)(1+\frac{1}{p_2}+\frac{1}{p^2_2}+\frac{1}{p^3_2}+\ldots) \\ \\ \text{Thus, for all primes $p\le z$ the sum can be written as} \\ \\ \ln{z} \le \sum\frac{1}{m} = \prod_{p\le z}({\sum_{k\ge 0}\frac{1}{p^{k}}}) \\ \text{where the inner sum }{\sum_{k\ge 0}\frac{1}{p^{k}}} \text{ is a geometric series with ratio }\frac{1}{p} \\ \ln{z} \le \prod_{p\le z}\frac{1}{1-\frac{1}{p}} \\ \ln{z} \le \prod_{p\le z}\frac{p}{p-1} \\\]4. Tricks of bounds
The bound on the product above $p \le z$ can be expressed in terms of primes indexed by $k$ where $k$ extends from the first prime ($k=1$) to the last prime, bounded by $\pi(z)$
\[\ln{z} \le \prod_{k=1}^{\pi(z)}\frac{p}{p-1} \\\]Examining the trends of primes and their respective indexes, at index $k=1,\ p_1=2$, at $k=2,\ p_2=3$, at $k=3,\ p_3=5$ and so on, leading to the observation that the primes grow faster than their index (enumeration), formally stated as:
\[p_k\ge k+1 \\ \text{Rearranging terms:}\\ p_k-1\ge k \\ \frac{1}{p_k-1}\le \frac{1}{k} \\ 1+\frac{1}{p_k-1}\le 1+\frac{1}{k} \\ \frac{p}{p_k-1}\le \frac{k+1}{k} \\\]Substituting this inequality in the product above:
\[\begin{equation} \ln{z} \le \prod_{k=1}^{\pi(z)}\frac{k+1}{k} \\ \text{But, }\prod_{k=1}^{\pi(z)}\frac{k+1}{k} = \frac{2}{1}+\frac{3}{2}+\frac{4}{3}+\ldots+\frac{\pi(z)-1}{\pi(z)-2}+\frac{\pi(z)}{\pi(z)-1}+\frac{\pi(z)+1}{\pi(z)}\\ \text{Alternate numerators and denominators cancel out, leaving:}\\ \prod_{k=1}^{\pi(z)}\frac{k+1}{k}=\pi(z)+1 \end{equation}\]Thus,
\[\ln{z}\le \pi(z)+1\]Since the natural logarithm is unbounded ($\ln{z}\rightarrow\infty$ as $z\rightarrow\infty$), we have a contradiction and $\pi(z)$ can not be bounded. Thus, $\pi(z)$ is unbounded and there are infinitely many primes.